堆是一种数据结构,而priority_queue (优先队列)是一个基于二叉堆的STL容器。
堆有很多种类,但以下提及的堆均为二叉堆。
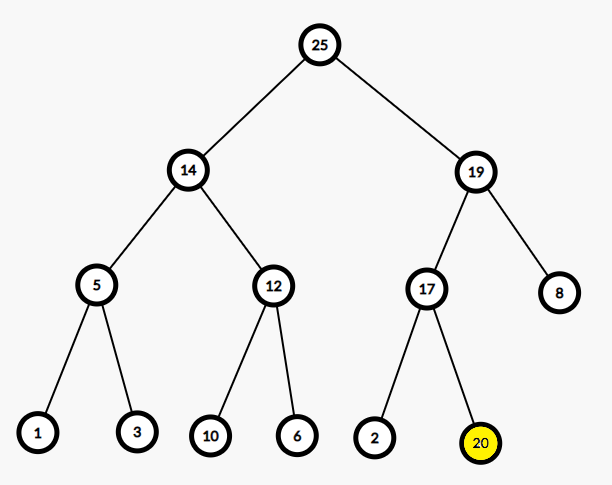
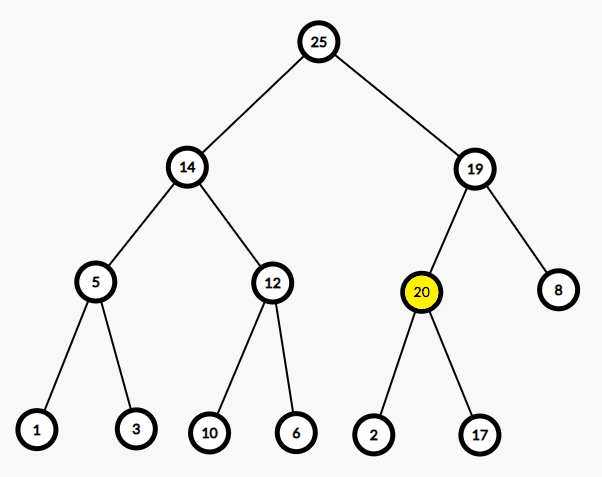
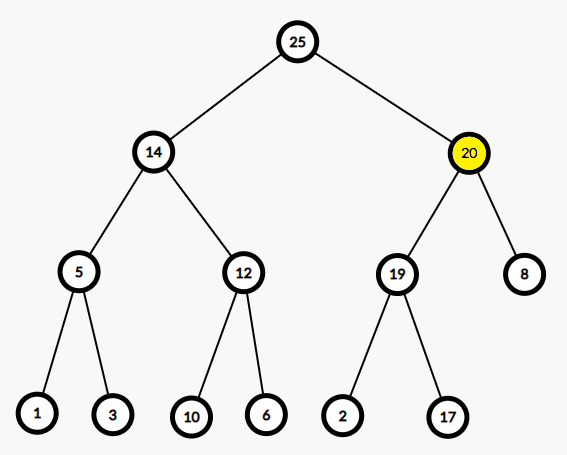
以下是一个例子。将新元素20插入二叉堆:
所以对一个二叉堆,有3种基本操作:
插入:将 val 插入堆。
取堆顶:查看堆顶元素值。(即整个堆中最大或最小值)
出堆:将堆顶元素出堆。
大根堆参考实现代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| struct Heap {
int heap[N], n;
void clear() { n = 0; }
void up(int p) {
while (p > 1) {
if (heap[p] > heap[p / 2]) {
swap(heap[p], heap[p / 2]);
p /= 2;
} else {
break;
}
}
}
void down(int p) {
int s = p * 2;
while (s <= n) {
if (s < n && heap[s] < heap[s + 1]) ++s;
if (heap[s] > heap[p]) {
swap(heap[s], heap[p]);
p = s;
s = p * 2;
} else {
break;
}
}
}
void insert(int val) {
heap[++n] = val;
up(n);
}
void pop() {
heap[1] = heap[n--];
down(1);
}
};
|
但在 C++ STL中,我们有 priority_queue 。所以我们通常就直接使用它,而不会手敲二叉堆(但是至少应该知道优先队列的工作原理)。
请注意 priority_queue 的堆顶默认是整个堆中的最大值(即默认大根堆,反过来的叫小根堆)。
priority_queue 有以下方法:
push(val): 将 val 插入堆。$O(logN)$top(): 查看堆顶元素值。(即整个堆中最大或最小值)$O(1)$pop(): 将堆顶元素出堆。$O(logN)$size(): 取堆大小。$O(1)$empty(): 判断堆是否为空。$O(1)$
有时我们需要(重新)定义小于号以使用 priority_queue 。有很多种方法可以实现对小于号的重载,如
bool operator<friend bool operator<bool operator()
以下是练习题:
POJ-1338, HDOJ-4006, POJ-3253, HDOJ-1873, HDOJ-1509, POJ-1442, HDOJ-1896, POJ-1456
另外,与二叉堆关系密切的一个经典问题是: 哈夫曼树 (Huffman Tree). 如 T^TOJ-3810.
部分练习题参考代码
POJ-1338 [Ugly Numbers] 参考代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #include <stdio.h>
#include <queue>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
priority_queue<LL, vector<LL>, greater<LL> > q;
vector<LL> v;
int main() {
int n;
q.push(1);
while (q.size() < 1500) {
LL val = q.top();
q.pop();
if (!v.empty() && v.back() == val) continue;
v.push_back(val);
q.push(val * 2);
q.push(val * 3);
q.push(val * 5);
}
while (~scanf("%d", &n) && n) {
printf("%lld\n", v[n - 1]);
}
return 0;
}
|
HDOJ-4006 [The kth great number] 参考代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| #include <stdio.h>
#include <queue>
using namespace std;
int main() {
int n, k, num;
char op[3];
while (~scanf("%d %d", &n, &k)) {
priority_queue<int, vector<int>, greater<int> > q;
while (n--) {
while (q.size() > k) q.pop();
scanf("%s", op);
if (op[0] == 'I') {
scanf("%d", &num);
q.push(num);
} else {
printf("%d\n", q.top());
}
}
}
return 0;
}
|